在计算机科学与数学中,一个排序算法(Sorting algorithm)是一种能将一串数据依照特定排序方式的一种算法。最常用到的排序方式是数值顺序以及字典顺序。有效的排序算法在一些算法(例如搜索算法与合并算法)中是重要的,如此这些算法才能得到正确解答。排序算法也用在处理文字数据以及产生人类可读的输出结果。基本上,排序算法的输出必须遵守下列两个原则:
- 输出结果为递增串行(递增是针对所需的排序顺序而言)
- 输出结果是原输入的一种排列、或是重组
虽然排序算法是一个简单的问题,但是从计算机科学发展以来,在此问题上已经有大量的研究。举例而言,冒泡排序在1956年就已经被研究。虽然大部分人认为这是一个已经被解决的问题,有用的新算法仍在不断的被发明。(例子:图书馆排序在2004年被发表)
分类
在计算机科学所使用的排序算法通常被分类为:
- 计算的复杂度(最差、平均、和最好性能),依据列表(list)的大小(n)。一般而言,好的性能是O(n log n),且坏的性能是O(n2)。对于一个排序理想的性能是O(n)。仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要O(n log n)。
- 存储器使用量(以及其他电脑资源的使用)
- 稳定度:稳定排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。也就是一个排序算法是稳定的,就是当有两个有相等关键的纪录R和S,且在原本的列表中R出现在S之前,在排序过的列表中R也将会是在S之前。
- 一般的方法:插入、交换、选择、合并等等。交换排序包含冒泡排序和快速排序。选择排序包含希尔排序和堆排序。
稳定度
当相等的元素是无法分辨的,比如像是整数,稳定度并不是一个问题。然而,假设以下的数对将要以他们的第一个数字来排序。
(4, 1) (3, 1) (3, 7) (5, 6)
在这个状况下,有可能产生两种不同的结果,一个是依照相等的键值维持相对的次序,而另外一个则没有:
(3, 1) (3, 7) (4, 1) (5, 6) (维持次序)(3, 7) (3, 1) (4, 1) (5, 6) (次序被改变)
不稳定排序算法可能会在相等的键值中改变纪录的相对次序,但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩充键值的比较,如此在其他方面相同键值的两个对象间之比较,(比如上面的比较中加入第二个标准:第二个键值的大小)就会被决定使用在原先数据次序中的条目,当作一个同分决赛。然而,要记住这种次序通常牵涉到额外的空间负担。
排列算法列表
在这个表格中,n是要被排序的纪录数量以及k是不同键值的数量。
稳定的
- 冒泡排序(bubble sort) — O(n2)
- 鸡尾酒排序 (Cocktail sort, 双向的冒泡排序) — O(n2)
- 插入排序 (insertion sort)— O(n2)
- 桶排序 (bucket sort)— O(n); 需要 O(k) 额外空间
- 计数排序 (counting sort) — O(n+k); 需要 O(n+k) 额外空间
- 合并排序 (merge sort)— O(n log n); 需要 O(n) 额外空间
- 原地合并排序 — O(n2)
- 二叉排序树排序 (Binary tree sort) — O(n log n)期望时间; O(n2)最坏时间; 需要 O(n) 额外空间
- 鸽巢排序 (Pigeonhole sort) — O(n+k); 需要 O(k) 额外空间
- 基数排序 (radix sort)— O(n·k); 需要 O(n) 额外空间
- Gnome 排序 — O(n2)
- 图书馆排序 — O(n log n) with high probability, 需要 (1+ε)n 额外空间
不稳定
- 选择排序 (selection sort)— O(n2)
- 希尔排序 (shell sort)— O(n log n) 如果使用最佳的现在版本
- 组合排序 — O(n log n)
- 堆排序 (heapsort)— O(n log n)
- 平滑排序 — O(n log n)
- 快速排序 (quicksort)— O(n log n) 期望时间, O(n2) 最坏情况; 对于大的、乱数列表一般相信是最快的已知排序
- Introsort — O(n log n)
- Patience sorting — O(n log n + k) 最坏情况时间,需要 额外的 O(n + k) 空间,也需要找到最长的递增子串行(longest increasing subsequence)
不实用的排序算法
- Bogo排序 — O(n × n!),最坏的情况下期望时间为无穷。
- Stupid sort — O(n3); 递归版本需要 O(n2) 额外存储器
- 珠排序(Bead sort) — O(n) or O(√n), 但需要特别的硬件
- Pancake sorting — O(n), 但需要特别的硬件
- [Stooge排序] 算法简单,但需要约n^2.7的时间
平均时间复杂度
平均时间复杂度由高到低为:
- 冒泡排序 O(n2)
- 插入排序 O(n2)
- 选择排序 O(n2)
- 归并排序 O(n log n)
- 堆排序 O(n log n)
- 快速排序 O(n log n)
- 希尔排序 O(n1.25)
- 基数排序 O(n)
说明:虽然完全逆序的情况下,快速排序会降到选择排序的速度,不过从概率角度来说(参考信息学理论,和概率学),不对算法做编程上优化时,快速排序的平均速度比堆排序要快一些。
简要比较
| 名称 | 数据对象 | 稳定性 | 时间复杂度 | 空间复杂度 | 描述 | ||
|---|---|---|---|---|---|---|---|
| 平均 | 最坏 | ||||||
| 插入排序 | 数组、链表 |  |  | (有序区,无序区)。把无序区的第一个元素插入到有序区的合适的位置。对数组:比较得少,换得多。 | |||
| 直接选择排序 | 数组 |  |  | (有序区,无序区)。在无序区里找一个最小的元素跟在有序区的后面。 对数组:比较得多,换得少。 | |||
| 链表 | |||||||
| 堆排序 | 数组 |  |  | (最大堆,有序区)。从堆顶把根卸出来放在有序区之前,再恢复堆。 | |||
| 归并排序 | 数组、链表 |  |  , 如果不是从下到上 , 如果不是从下到上 | 把数据分为两段,从两段中逐个选最小的元素移入新数据段的末尾。可从上到下或从下到上进行。 | |||
| 快速排序 | 数组 |  |  | 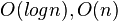 | (小数,枢纽元,大数)。 | ||
| Accum qsort | 链表 |  |  | 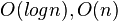 | (无序区,有序区)。把无序区分为(小数,枢纽元,大数),从后到前压入有序区。 | ||
| 决策树排序 | 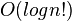 | 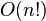 | O(n) <O(logn!) <O(nlogn) | ||||
| 计数排序 | 数组、链表 |  |  | 统计小于等于该元素值的元素的个数 i,于是该元素就放在目标数组的索引 i位。(i≥0) | |||
| 桶排序 | 数组、链表 |  |  | 将值为 i 的元素放入i 号桶,最后依次把桶里的元素倒出来。 | |||
| 基数排序 | 数组、链表 |  ,最坏: ,最坏: | 一种多关键字的排序算法,可用桶排序实现。 | ||||
- 均按从小到大排列
- k 代表数值中的"数位"个数
- n 代表数据规模
- m 代表数据的最大值减最小